Question

Find the value of x.Formula for area of a rectangle: A = LW

Answer 1

To answer this question, we need to identify the length and the width of the rectangle. We can say that the longest side is the length and the other side is the width.

Then, we can say:

`l=(x+1),w=(x+6)`

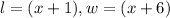
Since the area is:

`A_{\text{rectangle}}=lw,A=140`

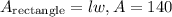
Then, we have:

`A_{\text{rectangle}}=(x+10)(x+6)=140`

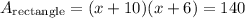
Now, we have a polynomial of second grade, and we need to find a valid value of x since we will have two solutions in this case.

Then, we have:

`(x+10)(x+6)=140`

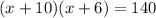
We can solve this equation using the quadratic formula to find the solutions:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

And we can apply it to the general form:

`ax^2+bx+c=0`

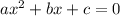
We need to expand the above expression as follows:

`(x+10)(x+6)=x^2+10x+6x+60=140`
`x^2+16x+60=140`
`x^2+16x+60-140=0\Rightarrow x^2+16x-80=0_{}`

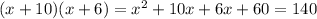
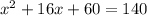
And we have that:

• a = 1

,

• b = 16

,

• c = -80

Now, we can find the solutions by substituting each of the values into the quadratic formula as follows:

`x=\frac{-16\pm\sqrt[]{(16)^2_{}-4(1)(-80)}}{2(1)}`
`x=\frac{-16\pm\sqrt[]{256+320}}{2}=\frac{-16\pm\sqrt[]{576}}{2}`
`x=\frac{-16\pm24_{}}{2}`

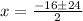
Then, the two possible solutions are:

`x=(-16+24)/(2)\Rightarrow x=(8)/(2)\Rightarrow x=4`

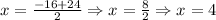
And

`x=(-16-24)/(2)\Rightarrow x=(-40)/(2)\Rightarrow x=-20`

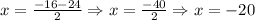
The area is a positive value. If we use each value, we will have:

For x = 4

`(x+6)(x+10)=(4+6)(4+10)=(10)(14)=140`

For x = -20

`(-20+6)(-20+10)=(-14)(-10)=140`

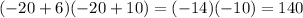
However, the length and the width must be positive numbers (the length is 14 units and the width equal to 10 units). Then, a valid value for x is 4.

In summary, we have that a valid value for x is 4, x = 4 (units).