Question

Below is the graph of a trigonometric function. It intersects its midline at (8.7, 7.2) and it has a minimumpoint at 6.2, 3.8). What is the period ?

Answer 1

The period is the value (in the x-axis) for the graph to go back to a given y value, in the same direction. Let's see a drawing:

The two red points in the drawig have the same y-value, and they are both placed in the curve in the place where it stops increasing to start to decrease.

So, in our case, we are given 2 points, a minimum (6.2, 3.8) and where the function intersects its midlines (8.7, 7.2).

We can see that the distance (in the x axis) between the minimum and the midpoint is one quarter of the period, why?:

- The period is the necessary distance to go from (6.2, 3.8) to another minimum (we can take the one in the left of the graph, near the point (-4, 3.8))

- At the midpoint we will be half way to get to a maximum (near the point (12, 10.5)

So, we need to find the distance between the minimum and the midpoint, and then multiply by 4 (let's call T the period):

`\begin{gathered} T=4\cdot\Delta x \\ T\text{ = 4}\cdot\text{(8.7-6.2) = 4}\cdot(2.5)=10 \end{gathered}`

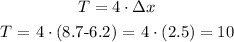
Where

`\Delta x`

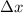
is the difference between the x-coordinate of the 2 points we are given.