Question

The perimeter of the rectangle below is 198 units. Find the length of side PS.Write your answer without variables.

Answer 1

PS = 47 units

Step-by-step explanation

We have the perimeter of this rectangle and we have to find the length of the side PS.

The perimeter of a rectangle is the sum of the lengths of the sides or the sum of twice each dimension - this is because the sides have the same length in pairs.

For this rectangle, we have that the perimeter is 198 units,

`2PS+2SR=198`

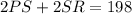
And sides PS and SR are (4y + 3) and (5y - 3) respectively. Replace into the equation above,

`2(4y+3)+2(5y-3)=198`

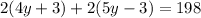
We have an equation for y. To solve it first we have to apply the distributive property,

`\begin{gathered} 2\cdot4y+2\cdot3+2\cdot5y-2\cdot3=198 \\ 8y+6+10y-6=198 \end{gathered}`

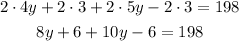
Then, add like terms,

`\begin{gathered} (8y+10y)+(6-6)=198 \\ 18y=198 \end{gathered}`

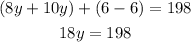
And finally, divide both sides by 18,

`\begin{gathered} (18y)/(18)=(198)/(18) \\ y=11 \end{gathered}`

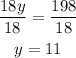
We now have y = 11, so we can replace it into the expression for the length of side PS,

`PS=4\cdot11+3=44+3=47\text{units}`

The length of the side PS is 47 units.