Question

A population of 850 beetles is growing each month at a rate of 7% 1 - Write an equation that expresses the number of Beatles at time x2 - how many Beatles will there be in 11 months 3 - how many months will the beetle population reach 100,000 how many years is that

Answer 1

1 - exponential growth formula:

`y=a(1+r)^x`

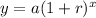
where:

y is the number of Beatles

a is the initial population of beetles

r is the rate (as a decimal)

x is time in moths

Replacing with a = 850, and r = 0.07, we get:

`\begin{gathered} y=850(1+0.07)^x^{} \\ y=850(1.07)^x \end{gathered}`

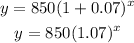
2 - Replacing with x = 11:

`y=850(1.07)^(11)\approx1789\text{ beetles}`

3 - Replacing with y = 100,000:

`\begin{gathered} 100000=850(1.07)^x \\ (100000)/(850)=(1.07)^x \\ \ln ((100000)/(850))=x\cdot\ln (1.07) \\ (\ln ((100000)/(850)))/(\ln (1.07))=x \\ 70.5\text{ months }\approx\text{ x} \end{gathered}`

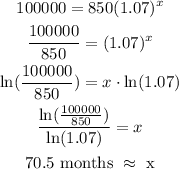
12 months is 1 year, then 70.5 months is equivalent to 70.5/12 = 5.875 years