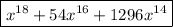Question

ose theWrite the first three terms in the binomial expansion, expressing the result in simplified form.1) (x2+6)9A) x18 +54x16 +2592x14C) x 18+60x16 +2592x14B) x18 +54x16+ 1296x14D) x18+ 60x16+ 1296x14

Answer 1

In this problem, we want to find the first three terms of this binomial expansion. There are several ways to approach this:

- attempt to multiply the terms

- use Pascal's Triangle

- use the Binomial Theorem

Since we only want the first three terms, we will use the binomial theorem, which states

`(a+b)^n=_nC_0a^nb^0+_nC_1a^(n-1)b^1+_nC_2a^(n-2)b^2+...+_nC_na^0b^n`

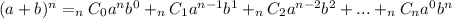
Where n represents the exponent of the binomial, and a and be represent the terms inside the parentheses. We use the combination function for the coefficients, n choose r objects.

From the given information, we know

`\begin{gathered} n=9 \\ \\ a=x^2 \\ \\ b=6 \end{gathered}`

To find the first 3 terms, we will substitute the given information into the formula:

`_9C_0(x^2)^96^0+_9C_1(x^2)^86^1+_9C_2(x^2)^76^2`

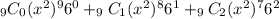
Simplifying the first term, we have

`_9C_0(x^2)^96^0=1\cdot x^(18)\cdot1=x^(18)`

The second term:

`_9C_1(x^2)^86^1=9\cdot x^(16)\cdot6=54x^(16)`

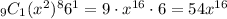
And the third term:

`_9C_2(x^2)^76^2=36\cdot x^(14)\cdot36=1296x^(14)`

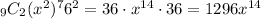
Putting each of those together, we get the first three terms:

`\boxed{x^(18)+54x^(16)+1296x^(14)}`