Question

FIND THE RATE CHANGE FOR FG AND OVER WHAT INTERVALS OF TIME IS MICHA TRAVELING THE FASTEST AND WHY ARE SOME LINE SEGMENTS ON THE GRAPH STEEPER THAN OTHERS

Answer 1

1.as we have differents slopes, it means he had differents speeds

2) rates of change

AB is 5

CD is 5

EF is -1.25

BC is 2.5

DE is 0

FG is -4.16666

3) AB and CD

Step-by-step explanation

when you have a graph where

x-axis=time

y-axis = distance

the rate of change is the speed, then

so

`\text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=speed`

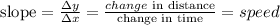
Step 1

why are some line segments on the graph sleeper than others?

as we have differents slopes, it means he had differents speeds

Step 2

speed of each line segment

a)rate of change AB

A=(0,0) origin

B=(4,20)

find the speed( slope)

`\text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=(y_2-y_1)/(x_2-x_1)=(20-0)/(4-0)=(20)/(4)=5`

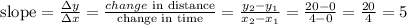
it means, the rate of change in AB is 5

b)rate of change CD

C=(12,40)

D=(16,60)

find the slope

`\text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=(y_2-y_1)/(x_2-x_1)=(60-40)/(16-12)=(20)/(4)=5`

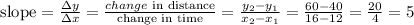
it means, the rate of change in CD is 5

c)rate of change EF

E=(20,60)

F=(28,50)

find the slope

`\text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=(y_2-y_1)/(x_2-x_1)=(50-60)/(28-20)=(-10)/(8)=-(5)/(4)=-1.25`

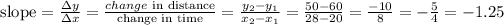
it means, the rate of change in EF is -1.25

d)rate of change BC

B=(4,20)

C=(12,40)

find the slope

`\text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=(y_2-y_1)/(x_2-x_1)=(40-20)/(12-4)=(20)/(8)=2.5`

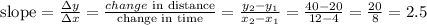
it means, the rate of change in BC is 2.5

e)Rate of change DE

D=(16,60)

E=(20,60)

find the slope

`\text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=(60-60)/(20-16)=(0)/(4)=0`

it means, the rate of change in DE is 0

f)rate of change change FG

F=(28,50)

G=(40,0)

find the slope

`\begin{gathered} \text{slope}=(\Delta y)/(\Delta x)=\frac{change\text{ in distance}}{\text{change in time}}=(0-50)/(40-28)=(-50)/(12)=-4.16666 \\ \end{gathered}`

it means, the rate of change in FG is -4.16666

Step 3

what interval is the fastest?

the fastest interval is when you have the bigger slope , then

`AB\text{ and CD}`

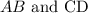
because the speed is 5