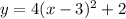We have that the vertex form of the equation of the parabola is the following:
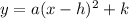
where (h,k) is the vertex of the parabola.
In this case, we have that the vertex is (h,k) = (3,2) and that the parabola passes through the point (x,y) = (4,6). Then, using the equation in vertex form, we have the following:
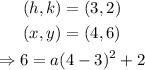
solving for 'a', we get:
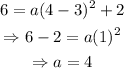
therefore, the equation of the parabola is: