Question

solve each trigonometric equation such as
`0 \leqslant x \leqslant 2\pi`give answers in exact form

Answer 1

Consider the given equation,

`\sqrt[]{2}\cos (x)+1=0`

Transpose the terms,

`\sqrt[]{2}\cos (x)=-1\Rightarrow\cos (x)=\frac{-1}{\sqrt[]{2}}`

Consider that the cosine function is negative in the 2nd and 3rd quadrant.

So one value of 'x' will lie in each quadrant.

Consider that 'x' lies in the 2nd quadrant,

`\cos (x)=\cos (\pi-(\pi)/(4))\Rightarrow x=\pi-(\pi)/(4)\Rightarrow x=(3\pi)/(4)`

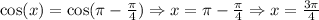
Consider that 'x' lies in the 3rd quadrant,

`\cos (x)=\cos (2\pi-(\pi)/(4))\Rightarrow x=2\pi-(\pi)/(4)\Rightarrow x=(7\pi)/(4)`

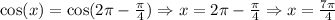
Thus, the two solutions of the equation are obtained.