Question

The height h(in feet) of a project tile with an initial vertical Velocity of 96 feet/seconds is modeled by the function h=-16t^2+96t, where t is the time, in seconds Answer the following

Answer 1

The function of the height is,

`h=-16t^2+96t`

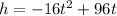
where,

`t=\text{time in seconds}`
`h=\text{height}`

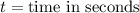
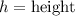
We will start substituting the values of t starting from when t= 0 till the function gives us negative.

Step 1:

`\begin{gathered} when\text{ t=0,} \\ h=-16(0)^2+96(0)=0+0=0ft \end{gathered}`
`\begin{gathered} \text{when t=1} \\ h=-16(1)^2+96(1)=-16+96=80ft \end{gathered}`
`\begin{gathered} \text{when t=2} \\ h=-16(2)^2+96(2)=-64+192=128ft \end{gathered}`
`\begin{gathered} \text{when t=3} \\ h=-16(3)^2+96(3)=-144+288=144ft \end{gathered}`
`\begin{gathered} \text{when t=4} \\ h=-16(4)^2+96(4)=-256+384=128ft \end{gathered}`
`\begin{gathered} \text{when t=5} \\ h=-16(5)^2+96(5)=-400+480=80ft \end{gathered}`
`\begin{gathered} \text{when t=6} \\ h=-16(6)^2+96(6)=-576+576=0ft \end{gathered}`
`\begin{gathered} \text{when t=7} \\ h=-16(7)^2+96(7)=-784+672=-112ft \end{gathered}`

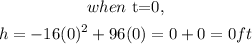
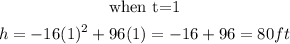
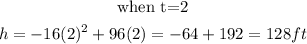
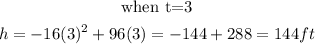
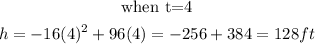
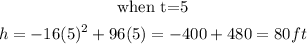
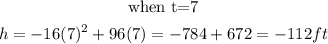
Step 2:

Step 3: We are to plot the graph and determine the highest point.

Hence, from the graph we can confirm that the time in which the projectile was in the air is 6seconds.