For two lines to be perpendicular, their slope must be negative reciprocal with each other.
So, for the line y = 2/3x - 4, the slope here is 2/3. Hence, the line perpendicular to this line must have a slope of -3/2.
To be able to find the equation that has a slope of -3/2 and passing through the point (0, 3), we can use the pattern below:

where m = slope and (x₁, y₁) is the coordinates of a point on the line.
Since we have a slope and a point already, let's plug it in to the pattern.
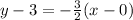
Then, solve for y.
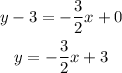
Hence, the equation of the line perpendicular to y = 2/3x - 4 passing through point (0,3) is y = -3/2x + 3.