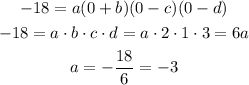Question

What is the value of the leading coefficient a if the polynomial function P(x) = a(x + b)(x − c)(x − d) passes through the points (–2, 0), (1, 0), (3, 0), and (0, –18)?

Answer 1

The polynomial equation is:

`P(x)=a(x+b)(x-c)(x-d)`

We want to find the value of a knowing that the points (-2,0), (1,0), (3, 0) and (0, -18) satisfy the equation.

The three first points are the roots of the polynomial, so we can easily say:

`b=2,c=1,d=3\text{ are the roots of the polynomial}`

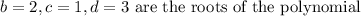
Now we can use this values and the last point to find the value of a:

`\begin{gathered} -18=a(0+b)(0-c)(0-d) \\ -18=a\cdot b\cdot c\cdot d=a\cdot2\cdot1\cdot3=6a \\ a=-(18)/(6)=-3 \end{gathered}`