We have to calculate the value of:

We have to look for the value of f(1/2) and f(3) in the definition of f(x).
For f(1/2), x is 1/2 and is between 0 and 3, so f(x) is:
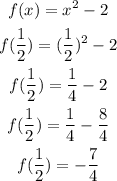
For f(3), it falls in the interval for x ≥ 3, so f(3) can be calculated as:
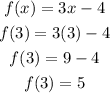
Then, we can now calculate the value of the expression as:
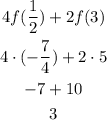
Answer: the expression is equal to 3.