Question

If 25.0 grams of Lithium reacts with 2.0 grams of Bromine... a. Balance the reaction. b. What type of reaction is this? c. What is the limiting reactant? d. What is the excess reactant? e. How much excess in grams?

Answer 1

The reaction between lithium and bromine gives us lithium bromide as a product. The balanced reaction is as follows:

`Li+Br_2\rightarrow2LiBr`

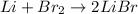
b. This is an oxidation-reduction reaction since there is a transfer of electrons between the elements. Br2 is an oxidizing agent and Li is the reducing agent.

`\begin{gathered} 2Br^0+2e^-\rightarrow2Br^(-I)(\text{Reduction)} \\ 2Li^0-2e^-\rightarrow2Li^I\text{ (Oxi}dation) \end{gathered}`

Now to determine the limiting reactant and the one that is in excess, we must determine the number of moles in the grams of reactants that we are given. For that, we will use the molar mass of the elements and find the moles as follows.

Moles of Lithium

`\begin{gathered} \text{Moles of Li=Given g of Li}*\frac{1molLi}{Molar\text{ Mass, g Li}} \\ \text{Moles of Li}=25.0gLi*\frac{1molLi}{6.941\text{g Li}}=3.6\text{mol Li} \end{gathered}`

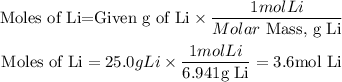
Moles of Bromine (Br2)

`\begin{gathered} MolesofBr=GivengofBr_2*\frac{1\text{mol}Br_2}{Molar\text{ Mass, g }Br_2} \\ \text{Moles of Br}=2.0gBr_2*\frac{1\text{mol}Br_2}{159.8\text{g }Br_2}=0.013\text{mol }Br_2 \end{gathered}`

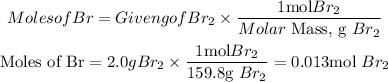
c. To determine the limiting reactant, we divide the moles of each reactant by the smallest number of moles that we find, that is, 0.013. The reactant with the lowest coefficient is the limiting reactant.

`\begin{gathered} Li\rightarrow(3.6)/(0.013)=76.9 \\ Br=(0.013)/(0.013)=1 \end{gathered}`

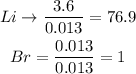
The limiting reactant will be the Bromine

d. So, the excess reactant will be Lithium

e.For every mole of Br2 that reacts, one mole of Li will react. Since bromine is the limiting reagent, 0.013 mol of Br and 0.013 mol of Li will react.

Therefore, the grams that will not react will be:

`\begin{gathered} \text{gLi}=(\text{Moles Li-Moles that reacts Li)}*\frac{MolarMass,\text{ gLi}}{1molLi} \\ \text{gLi}=(\text{3.6molLi-0.013molLi)}*\frac{6.941\text{ gLi}}{1molLi}=24.9g\text{ of Li} \end{gathered}`

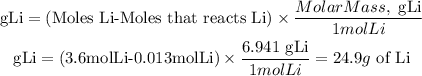
We have 24.9 g of Li in excess