Question

Question is in picture

Answer 1

`b)-3,\text{ -}(1)/(2)`

Step-by-step explanation

The zero of a function is any replacement for the variable that will produce an answer of zero,so to find the zeros of this function we need set the equation = 0, and then solve for x

`2x^2+7x+3=0`

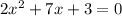
The rigth side of the equation is zero, so we can solve

`\begin{gathered} 2x^2+7x+3=0\Rightarrow ax^2+bx+c \\ \end{gathered}`

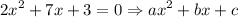
we can use the quadratic formula

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{replace} \\ x=\frac{-7\pm\sqrt[]{7^2-4\cdot2\cdot3}}{2\cdot2} \\ x=\frac{-7\pm\sqrt[]{49-24}}{4} \\ x=\frac{-7\pm\sqrt[]{25}}{4} \\ x=(-7\pm5)/(4) \end{gathered}`

therefore.

`\begin{gathered} x_1=(-7+5)/(4)=-(2)/(4)=-(1)/(2) \\ x_2=(-7-5)/(4)=-(12)/(4)=-3 \end{gathered}`

so, the answer is

`b)-3,\text{ -}(1)/(2)`

I hope this helps you