The Solution:
The question assumed that the readings on the thermometer are normally distributed with mean 0 degrees and standard deviation 1.00 degrees.
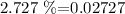
So, from the z-table, we have that
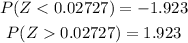
So, for readings that too low, we have
![\begin{gathered} P(ZFor readings that too high, we have[tex]\begin{gathered} P(Z<1.923)\Rightarrow Z=(x-\mu)/(\sigma) \\ \\ 1.923=(x-0)/(1) \\ \\ 1.923=x \end{gathered}]()
To draw a sketch that shows the two readings that are cutoff values of the rejected thermometer, we have