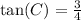Question

What is the ratio equivalent oftar (C)? hint: use the Pythagorean theorem to find the missing side

Answer 1

GivenHiven the Right Triangle ABC, you can find the missing side AB using the Pythagorean Theorem. This states that:

`c^2=a^2+b^2`

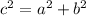
Where "c" is the hypotenuse, and "a" and "b" are the legs of the Right Triangle.

In this case:

`\begin{gathered} c=35 \\ a=28 \\ b=AB \end{gathered}`

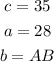
Then, substituting values and solving for AB, you get:

`(35)^2=(28)^2+(AB)^2`
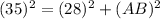
`\begin{gathered} \sqrt[]{(35)^2-(28)^2}=AB \\ \\ \sqrt[]{441}=AB \\ \\ AB=21 \end{gathered}`

By definition:

`\tan \alpha=(opposite)/(adjacent)`

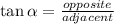
In this case, you can identify that:

`\begin{gathered} \alpha=C \\ opposite=AB=21 \\ adjacent=BC=28 \end{gathered}`

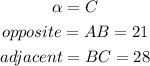
Therefore:

`\begin{gathered} \tan (C)=(21)/(28) \\ \\ \tan (C)=(3)/(4) \end{gathered}`

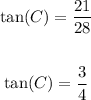
Hence, the answer is:

`\tan (C)=(3)/(4)`