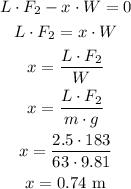ANSWER:
a) 63 kg
b) 0.74 m
Explanation:
Given:
F1 = 435 N
F2 = 183 N
L = 2.5 m
a)
Here the two forces F1 and F2 are actingupwards and his weight acting downwards.

By using the principles of torque we get:
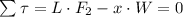
here x is the centerof the mass, solving and replacing for x: