Since the median divides the triangle ACD in two and they share an edge (the edge BD) we can use this information to try and find the angle mFor the triangle ABD we know that
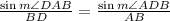
Now, since we know that

then the last equation simplifies to
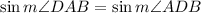
therefore m
 For the triangle BDC we know that
For the triangle BDC we know that
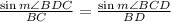
but since the segment DB is the median, this means that AB is equal to BC, furthermore we know that AB is equal to DB, this means that

so, the last law of sines simplifies to
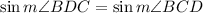
That implies that
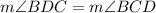
Now we have to notice that the angle m
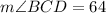 Finally we can conclude that the angle we are looking for is 32°.
Finally we can conclude that the angle we are looking for is 32°.