Answer:
$5
Explanation:
We are given that profit equation
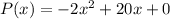
Where x=Charges per pair of mittens
We have to find the charge per pair of mittens to make her max profit.
Differentiate equation w.r.t x
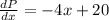
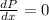
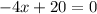
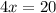
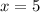
Again differentiate w.r.t x
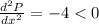
Hence, the profit is maximum at x=5
Lily should charge $5 per pair of mittens to make her max profit .