Question

Select the correct answer.Which function has exactly one real solution?-75A. f(t) = 6x2 + 11B. f(x) = –3r2 + 301C. f(x) = 2x2 + 4x – 5D. (t) = -4r2 + 9r

Answer 1

The number of solutions of a quadratic equations can be found by finding its delta. If it is positive, then there are two real solutions, if the delta is zero then there is only one real solution and if the it is negative then there are no real solutions. The expression for the delta is:

`\Delta=b^2-4ac`

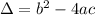
Let's check for which problems we have Delta equal to 0.

A.

`\Delta=0^2-4(6)\cdot(11)=-264`

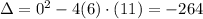
Since the Delta is less than 0, the quadratic function has no real solutions.

B.

`\Delta=0^2-4(-3)(301)=3612`

Since the Delta is greater than 0, he quadratic funcion has two real solutions.

C.