The area of a rectangle is the product of its length and its width.
Since the area of the rectangle is given by th polynomial function:
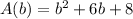
And the width of the rectangle is given by the binomial:
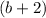
Factor out (b+2) from the expression of the area to find the other binomial factor, which corresponds to the length.
To do so, notice that the coefficient of b^2 is 1 and the constant term is 8. The product of those two numbers, 1 and 8, is 8.
The factors of 8 that sum to 6 are 2 and 4. Then, write the term 6b as 2b+4b:
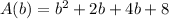
Factor b from th first two terms and 4 from the last two terms:
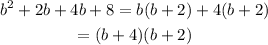
If we identify (b+4) as the length of the rectangle we can see that the area is given by the product of (b+4) and (b+2), which are the length and the width of the rectangle.
Therefore, the length of the rectangle is:
