Question

Explain whether the following could be true: In a survey of 223 students, 113 were taking algebra, 87 were taking biology, and 23 were taking neither of the two subjects.Choose the correct answer below and, if necessary, fill in any answer boxes to complete your choice. Use venn diagramA.No this could not be true because if students are taking neither of the two subjects then the distribution of students implies there will have to be more than total students.B.Yes this could be true if there were ?students taking algebra but not biology, and there were ?students taking biology but not algebra.

Answer 1

Given that

`\begin{gathered} n|A|only=113-x \\ n|B|only=87-x \\ n(A\cap B)^(\prime)=23 \\ n(A\cap B)=x \\ \cup=223 \end{gathered}`

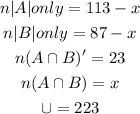
The Venn diagram will be shown below

Therefore,

`\begin{gathered} 113-x+x+87-x+23=223 \\ 113+87+23-x+x-x=223 \\ 223-x=223 \\ 223-223=x \\ 0=x \\ \therefore x=0 \end{gathered}`

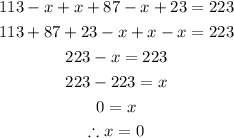
From the calculations done above, we can see that there is no intersection between the students that took algebra and biology.

Hence, the correct option is Option B.

Yes, this could be true if there were 113 students taking algebra but not biology, and there were 87 students taking biology but not algebra.