Category ------------ Nuclear chemistry
Sub-category --------- Radioactivity
ANSWER
The remaining amount of isotope after 1600 years is 32.9444 grams
Step-by-step explanation
Given that;
The half life of the isotope is 5715 years
The initial mass of the isotope is 40 grams
The decay time is 1600 years
Follow the steps below to find the remaining mass after 1600 years
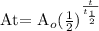
Where
A(t) is the amount of mass remaining after time t
Ao is the initial amount of mass of the substance
t1/2 is the half-life of the substance
t is the decay time
Substitute the given data into the above formula
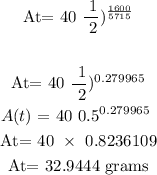
Therefore, the remaining amount of isotope after 1600 years is 32.9444 grams