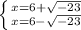Question

Solve x^2-12x+59=0 for x

Answer 1

C in simple terms

Explanation:

Answer 2

You can solve this using the Quadratic Formula, x =
`\frac{b (+ or -) \sqrt{ B^(2)-4ac}}{2a}`.
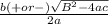
a = 1, b = -12, c = 59

x =
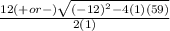
`\frac{12 (+ or -) \sqrt{(-12)^(2) -4(1)(59)} }{2(1)}` Multiply 4 and 1
x =
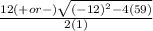
`\frac{12 (+ or -) \sqrt{(-12)^(2) -4(59)} }{2(1)}` Multiply 2 and 1
x =
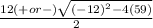
`\frac{12 (+ or -) \sqrt{(-12)^(2) -4(59)} }{2}` Multiply -4 and 59
x =
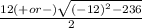
`\frac{12 (+ or -) \sqrt{(-12)^(2) -236} }{2}` Square 12
x =
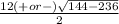
`(12 (+ or -) √(144 - 236) )/(2)` Subtract
x =
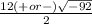
`(12 (+ or -) √(-92) )/(2)` You can't find the square root of negatives, so factor the -92 out.
x =
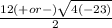
`(12 (+ or -) √(4 (-23)) )/(2)` You can find the sqaure of 4, so take that out.
x =
`(12 (+ or -) 2 √(-23) )/(2)` Split the expression into two parts
x =
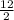
`(12)/(2)` (+ or -)
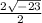
`(2 √(-23) )/(2)` The 2 in the numerator and the 2 in the denominator cancel each other out
x =
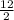
`(12)/(2)` (+ or -)
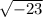
`√(-23)` Divide 12 by 2
x = 6 (+ or -)
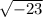
`√(-23)` Now, split the solution into the plus and minus parts.


`\left \{ {{x = 6 + √(-23) } \atop {x = 6 - √(-23) }} \right.`