Given:
The equation of the curve is given as,
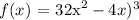
The required line is the tangent to the given curve at the point (1, -24).
Required:
Equation of the line tangent to the given curve.
Step-by-step explanation:
Differentiating the given function with respect to x,
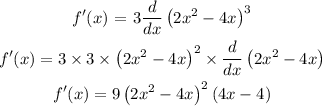
Slope of the tangent at (1,-24) is calculated as,
![\begin{gathered} f^(\prime)(x)\text{ at \lparen1,-24\rparen = 9}*[2\left(1\right)^2-4(1)]^2*[4(1)-4] \\ f^(\prime)(x)\text{ at \lparen1,-24\rparen = 9}*[2-4]*[4-4] \\ f^(\prime)(x)\text{ at \lparen1,-24\rparen = 9}*-2*0\text{ } \\ f^(\prime)(x)\text{ at \lparen1,-24\rparen = 0} \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/lf1l3xoqu1rdusmv7d3a.png)
Equation of the required line is given as,
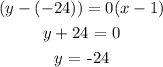
Answer:
Thus the equation of the required line is
