We will have the following:
We will have that the electrostatic force:

Now, for all SI units we will have that the constant is almost exactly 9*19^9 m/farad; so the force on each mass will be:
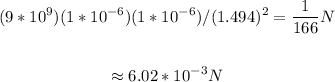
Now, we find the acceleration; that is:

Now, we will have that if both charges have opposite signs then the acceleration of ach mass is approximately 0.0127 m/s^2 in the direction toward the other.
If both charges have the same sign, then the acceleration will be approximately 0.0127m/s^2 in the direction away from the other.