Question

Write a recursive formula for each sequence.81,85,89,93,97

Answer 1

Write a recursive formula for each sequence:

`81,85,89,93,97`

To determine if the sequence is said to be constant, arithmetic sequence can be solve by checking the difference between two consecutive terms

`\begin{gathered} T_1=firstterm=81 \\ T_2=\sec ondterm=85 \\ T_3=thirdterm=89_{} \\ T_4=fourthterm=93 \\ T_5=fifthterm=97 \end{gathered}`

Common difference is the diffrence between the first term and second term or the second term and third term.

`a=\text{first term }`

`\begin{gathered} 85-81=89-85=93-89=97-93=4 \\ \text{Arithmetic sequence formula=} \\ T_n=a+(n-1)d \\ T_n=T_1+(n-1)d \\ T_n=81+(n-1)4 \\ T_n=81+4n-4 \\ T_n=81-4+4n \\ T_n=77+4n \end{gathered}`

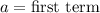
Hence the recursive formula for each sequence = 77 + 4n