Question

Carbon-14 is used to determine the time an organism was living. The amount of carbon-14 an organism has is constant with the atmosphere, but when an organism dies the carbon-14 decays at a half-life of 5,730 years. If an archeologist measured the amount of carbon-14 in an organism and it was 25% of the total amount of atmospheric C-14, what is the age of the organism? 1432.5 years 5,730 years 11,460 years 17,190 years

Answer 1

8

Step-by-step explanation:

Answer 2

The age of the organism is approximately 11460 years.

Step-by-step explanation:

The amount of carbon-14 decays exponentially in time and is defined by the following equation:

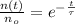`(n(t))/(n_(o)) = e^{-(t)/(\tau) }` (1)

Where:

`n_(o)` - Initial amount of carbon-14.

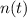`n(t)` - Current amount of carbon-14.

`t` - Time, measured in years.

`\tau` - Time constant, measured in years.

Then, we clear the time within the formula:

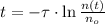`t = -\tau \cdot \ln (n(t))/(n_(o))` (2)

In addition, time constant can be calculated by means of half-life of carbon-14 (
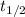`t_(1/2)`), measured in years:

`\tau = (t_(1/2))/(\ln 2)`

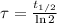
If we know that
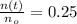`(n(t))/(n_(o)) = 0.25` and
`t_(1/2) = 5730\,yr`, then the age of the organism is:

`\tau = (5730\,yr)/(\ln 2)`

`\tau \approx 8266.643\,yr`

`t = -(8266.643\,yr)\cdot \ln 0.25`

`t \approx 11460.001\,yr`

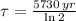
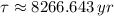
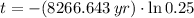
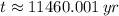
The age of the organism is approximately 11460 years.