Question

The endpoints of line AB are A(2, 2) and B(3, 8). Line AB is dilated by a scale factor of 3.5 with the origin as the center of dilation to give image line A'B' . What are the slope (m) and length of line AB? Use the distance formula to help you decide: . A. m=21, A'B'=3.5 √37

B. m=6, A'B'= √37
C. m=6, A'B'=3.5√37
D. m=21, A'B'=√37
E. m=6,A'B'=6√37

Answer 1

Option C - m=6, A'B'=3.5√37

Explanation:

Given : The endpoints of line AB are A(2, 2) and B(3, 8). Line AB is dilated by a scale factor of 3.5 with the origin as the center of dilation to give image line A'B' .

To find : What are the slope (m) and length of line AB?

Solution :

The slope of a line does not change.

Slope formula is
`m=(y_2-y_1)/(x_2-x_1)`

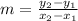
The slope of AB is :

`m=(8-2)/(3-2)`

`m=(6)/(1)`

`m=6`

Line AB is dilated by a scale factor of 3.5.

The length of AB by distance formula,

Distance formula,
`d = √((x_2-x_1)^2 + (y_2-y_1)^2)`

`d = √((3 - 2)^2 + (8 - 2)^2)`

`d = √((1)^2 + (6)^2)`

`d = √(1+36)`

`d = √(37)`

The length of A'B' is :

`d' =3.5*  √(37)`

`d' =3.5√(37)`

Therefore, The slope is m=6 and length of line is
`d' =3.5√(37)`

Hence, Option C is correct.

Answer 2

A` ( 7, 7 )
B ` ( 10.5, 28 )
The slope: m = (28-7) / ( 10.5 - 7 ) = 21 / 3.5 = 6
d ( A` B `) = √ ( 10.5 - 7 )² + ( 28 - 7 )² = √ 3.5² + 21² =
= √ 12.25 + 441 = √ 12.25 ( 1 + 36 ) = 3.5 √37 ( or 3.5 * (37) ^(1/2))
Answer:
C ) m = 6, A`B` = 3.5√37