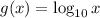Question

Write the function rule for g.(X) g(x)10. 1100. 21000 310000 4100000 5

Answer 1

We can see that the values of x are increasing exponentially, and are multiples of 10, and the values of g(x) increases unit by unit.

So let's use the model of an logarithm function, since it's the inverse of an exponential function.

If the value x = 10 gives a value of g(x) = 1, we can use the base 10 for the logarithm:

`g(x)=\log _(10)x`

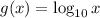
Checking the other values, we have:

`\begin{gathered} x=100\to g(100)=\log _(10)100=2 \\ x=1000\to g(1000)=\log _(10)1000=3 \\ x=10000\to g(10000)=\log _(10)10000=4 \\ x=100000\to g(100000)=\log _(10)100000=5 \end{gathered}`

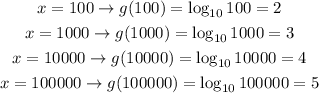
So the function is:

`g(x)=\log _(10)x`