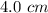Question

The longest side of an acute isosceles triangle is 8 centimeters. Rounded to the nearest tenth, what is the smallest possible length of one of the two congruent sides

Answer 1

Let

x------> the length of one of the two congruent sides of the isosceles triangle

we know that

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side

In this problem

the longest side is
`8\ cm`

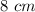
so

Applying the triangle inequality theorem

`x+x > 8`

`2x> 8`

`x> 4\ cm`

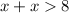
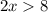
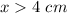
The length of one of the two congruent sides must be greater than
`4\ cm`

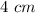
A solution could be
`4.01\ cm`

If you round to the nearest tenth
`4.01\ cm` the result is equal to
`4.0\ cm`

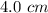
therefore

the answer is

the smallest possible length is
`4.0\ cm`

Answer 2

-- If the two congruent sides are any shorter than 4 cm, then
they can't reach end-to-end on the 8-cm side.

-- If they're exactly 4 cm, then they lie right on top of the 8 cm side,
and the triangle looks like a line segment that's 8 cm long.

-- The two congruent sides must be more than 4 centimeters long.

There's no such thing as their "smallest possible length". It can be
anything, just as long as it's more than 4 cm.

Whatever length that you name, no matter how close it is to 4 cm,
I can always name a shorter length that's still more than 4 cm.

So when it's rounded to the nearest tenth, hundredth, thousandth,
millionth etc., it's 4 cm.