Question

What is cos(npi/2) and sin(npi/2) in fourier series cos(npi) is (-1)^n and sin(npi)=0 ?

Answer 1

We have been given two function:

`cos(\frac{n{\pi}}{2})\text{and} sin(\frac{n{\pi}}{2})`

We need to tell their values so,

`cos(\frac{n{\pi}}{2})= \left \{ {{-1^{(n)/(2)}};\text{n is even} \atop {0};\text{n is odd}} \right.`

Put n=2 in the given above function cos(\frac{n{\pi}}{2}) we get: -1

Put n=3 in the function cos(\frac{n{\pi}}{2}) we get: 0

`sin(\frac{n{\pi}}{2})=\left \{ {{-1^{(n+3)/(2)}};\text{n is odd} \atop {0};\text{n is even}} \right.`

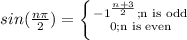
Put n=2 in the given above function cos(\frac{n{\pi}}{2}) we get: 0

Put n=3 in the function cos(\frac{n{\pi}}{2}) we get: -1

Answer 2

The problem ask to fourier series of the trigonometric function base on the data you have been given in the problem, so the answer would be cos(pi/2n) = {(-1)^n/2 - if n is even, 0 - if n is odd} and sin(pi/2n) = {0- if n is even, (-1)^(n-1)/2 if n is odd}. I hope you are satisfied with my answer