Question

Graph the quadratic equation X^2+5x+6. Explain and locate where your roots are.

Answer 1

We have to graph the quadratic equation defined as:

`y=x^2+5x+6`

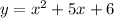
We can already identify that:

• The parabola opens upward (a > 0).

,

• The y-intercept is y = 6 (c = 6).

We can use the quadratic formula to find the roots:

`\begin{gathered} x=(-5\pm√(5^2-4(1)(6)))/(2(1)) \\ x=(-5\pm√(25-24))/(2) \\ x=(-5\pm√(1))/(2) \\ \to x_1=(-5-1)/(2)=-(6)/(2)=-3 \\ \to x_2=(-5+1)/(2)=-(4)/(2)=-2 \end{gathered}`

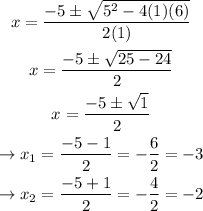
The roots are x = -3 and x = -2.

We can graph the parabola with these 3 points as:

Answer: The roots are located at x = -3 and x= -2.