Question

Factor each and find all roots. x^3+ 27 = 0

Answer 1

To factor the expression:

`x^3+27`

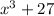
we need to notice that this is equal to:

`x^3+27=x^3+3^3`

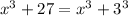
then we have a sum of cubes. A sum of cubes can always be factor as:

`x^3+y^3=(x+y)(x^2-xy+y^2)`

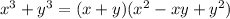
Then we can factor the expression as:

`x^3+27=(x+3)(x^2-3x+9)`

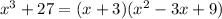
To find the roots we equal the factor expression to zero and solve for x:

`(x+3)(x^2-3x+9)=0`

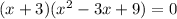
This equation implies that:

`\begin{gathered} x+3=0 \\ or \\ x^2-3x+9=0 \end{gathered}`

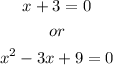
The first equation can be solved as:

`\begin{gathered} x+3=0 \\ x=-3 \end{gathered}`

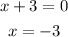
The second one can be solve as: