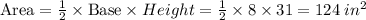Question

Set up an equation and solve the problem The area of a triangle sheet of paper is 124 square inches. One side of the triangle is 7 inches more than three times the length of the altitude to that side find the length of that side and the altitude to the sideSide. InAltitude. In

Answer 1

• Altitude = 8 inches

,

• Side = 31 inches

Step-by-step explanation:

Let the altitude to the given side = x inches

One side of the triangle is 7 inches more than 3 times the length of the altitude.

• Length of the side = (3x+7) inches

,

• The area if the triangle = 124 square inches

If the altitude is to the given side, then the given side is the base of the triangle.

`\begin{gathered} \text{Area}=(1)/(2)*\text{Base}* Height \\ 124=(1)/(2)(3x+7)(x) \end{gathered}`

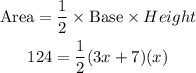
We then solve for x:

`\begin{gathered} 124*2=3x^2+7x \\ 248=3x^2+7x \\ 3x^2+7x-248=0 \end{gathered}`

Since the equation is quadratic, we solve it using the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\; where\; a=3,b=7,c=-248 \\ =\frac{-7\pm\sqrt[]{7^2-4(3)(-248)}}{2*3}=\frac{-7\pm\sqrt[]{49-(-2976)}}{6} \\ =\frac{-7\pm\sqrt[]{49+2976}}{6}=\frac{-7\pm\sqrt[]{3025}}{6} \\ =(-7\pm55)/(6) \end{gathered}`

Therefore, the values of x are:

`\begin{gathered} x=(-7-55)/(6)\text{ or x}=(-7+55)/(6) \\ x=-(62)/(6)\text{ or x }=(48)/(6) \\ \text{ x }=8\text{ inches (x cannot be negative)} \end{gathered}`

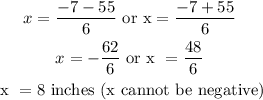
Thus, we have that:

• Length of the altitude = 8 inches

,

• Length of the side = (3x+7)=3(8)+7=31 inches

CHECK

`\text{Area}=(1)/(2)*\text{Base}* Height=(1)/(2)*8*31=124\; in^2`