Question

The time to complete a standardized exam is approximately normal with a mean of 70 minutes & a standard deviation of 10 minutes. Using the 68-95-99.7 rule, if students are given 90 minutes to complete the exam, what percentage of students will not finish?. A. 32%. B. 5%. C. 2.5%. D. 0.0015%. . Show step-by-step solution.

Answer 1

Option C) 2.5%

Explanation:

We are given the following information in the question:

The distribution of time to complete a standardized exam is approximately normal.

• The empirical rule states that for a normal distribution,the data will fall within three standard deviations of the mean.

• 68% of data falls within the first standard deviation from the mean that is
  `\mu \pm \sigma`

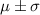
• 95% fall within two standard deviations that is
  `\mu \pm 2\sigma`

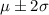
• 99.7% fall within three standard deviations that is
  `\mu \pm 3\sigma`

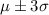
The students are given 90 minutes to complete the exam.

`90 = 70 + 2(10) = \mu + 2\sigma`

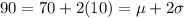
Around 95% of the students will fall in this interval
`\mu \pm 2\sigma`.

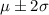Around 5% will not fall into this interval.

Thus, around 2.5% of the students will not be able to complete their test in 90 minutes.

We considered 2.5% only because the remaining 5% of students would lie on both sides of the mean. Our requirement was only to calculate students who would not be able to complete test even in 9- minutes so we divided this percentage by 2.

Answer 2

if the mean is 70 minutes, then 90 minutes is 2 standard deviations above 70. if you look at the bell curve i drew, the percent of exams that took over 90 minutes is 2.5%