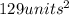Finding the surface area of the first regular prism.
The regular prism we have is:
To find the surface area, we need to find the area of the top which would be the same as the area of the bottom, and we also need to find the area of the sides.
Step 1. Let's start finding the area of the sides.
The prism has 6 sides, each of them is a rectangle with a base of 2 and a height of 9.
To find the area of just one side, we multiply the base of the rectangle by its height:
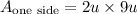
Where u represents units.
The result is:
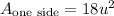
Since we have 6 equal rectangles in the surface area, we multiply the previous result by 6:
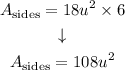
Step 2. Now we need to find the area of the hexagon at the top and bottom of the prism.
For that, we use the formula:

Where P is the perimeter and a is the apothem of the hexagon.
To find the apothem in a hexagon we use the following property:
The apothem is the red line, and since the triangle formed inside the hexagon is 30-60-90 triangle, we use the property shown in the diagram to find it.
In this case, one side of the hexagon has a length of 2 units. The base of the triangle shown in the diagram is half of one side, thus x is equal to 1 unit:
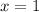
And the apothem then is:
![\begin{gathered} a=x\sqrt[]{3} \\ a=1u\sqrt[]{3} \\ a=\sqrt[]{3}u \\ a=1.73u \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ccw4fiva2bun2a1qhi3k.png)
Step 3. To find the area of the hexagon, we need perimeter:
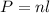
where n is the number of sides and l is the length of each side. In this case:

Step 4. Go back to the formula from step 2 and find the area of the hexagon:

Substituting P and a:

The result is:
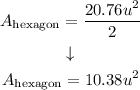
Step 5. Find the total surface area.
The total surface area will be the area of the sides plus the area of the two hexagons:
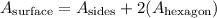
Substituting the known values:
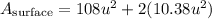
Solving the operations:
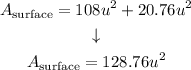
This can be round to 129 units squared:
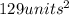
Answer: