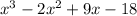Question

Which of the following is a polynomial with roots 2, –3i, and 3i ?.options:

A] x3 + 4x2 + 9x + 24

B] x3 – 4x2 + 9x – 24

C] x3 + 2x2 + 9x + 18

D] x3 – 2x2 + 9x – 18

Answer 1

The polynomial with roots 2, –3i, and 3i is:

`x^3-2x^2+9x-18`

Explanation:

We are given three roots of a polynomial as:

2, -3i, 3i

Let p(x) be the polynomial whose roots are defined above.

Now we can find the equation of the polynomial as follows:

`p(x)=(x-2)(x-3i)(x+3i)\\\\\\\i.e.\\\\\\p(x)=(x-2)(x^2-(3i)^2)\\\\\\p(x)=(x-2)(x^2-9i^2)\\\\\\p(x)=(x-2)(x^2+9)\\\\\\p(x)=x(x^2+9)-2(x^2+9)\\\\\\p(x)=x^3+9x-2x^2-18\\\\\\p(x)=x^3-2x^2+9x-18`

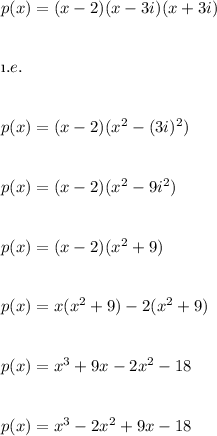
Hence, the answer is: Option: D

The polynomial is:
`x^3-2x^2+9x-18`

Answer 2

Out of the following choices, x3 – 2x2 + 9x – 18 is a polynomial with roots 2,-3i, and 3i. The correct answer is D.