Question

Find the vertex of the parabola whose equation is y = x^2 + 8x + 12.

Answer 1

The vertex of the parabola is (-4,-4).

Explanation:

If a quadratic function is defined as

`y=ax^2+bx+c` ... (1)

Then the vertex of the function is

`Vertex=((-b)/(2a),f((-b)/(2a)))`

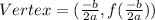
The given function is

`y=x^2+8x+12` .... (2)

From (1) and (2), we get a=1,b=8 and c=12.

`(-b)/(2a)=(-8)/(2(1))=-4`

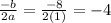
Substitute x=-4 in the given equation.

`f((-b)/(2a))=f(-4)=y=(-4)^2+8(-4)+12`

`y=16-32+12=-4`

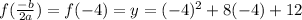
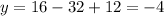
Therefore the vertex of the parabola is (-4,-4).

Answer 2

The vertex of a parabola is the point where the parabola crosses its axis of symmetry. If the coefficient of the x 2 term is positive, the vertex will be the lowest point on the graph, the point at the bottom of the “ U ”-shape.

The vertex of the parabola whose equation is y = x^2 + 8 x + 12 will be :
(x , y) = (-4,-4)