Question

I need help with this problem and solving it down step by step

Answer 1

To verifying if two functions are inverses of each other is a simple two-step process.

Step 1:

Plug g(x) into f(x) which is f{g(x)} then simplify.

If f{g(x)} = x

`\begin{gathered} f(x)\text{ = 9x + 12} \\ g(x)\text{ = }\frac{x\text{ - 12}}{9} \\ f\mleft\lbrace g(x\mright)\}\text{ = 9(}\frac{x\text{ - 12}}{9})\text{ + 12} \\ =\text{ x - 12 + 12} \\ f\mleft\lbrace g(x\mright)\}\text{ = x} \end{gathered}`

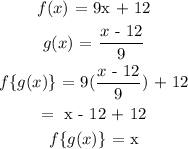
Step 2: g[f(x)] = x

`\begin{gathered} g\mleft\lbrace f(x\mright)\}\text{ = }\frac{9x\text{ + 12 - 12}}{9} \\ g\mleft\lbrace f(x\mright)\}\text{ = }(9x)/(9) \\ g\mleft\lbrace f(x\mright)\}\text{ = x} \end{gathered}`

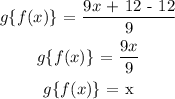
Final answer

Since f{g(x)} = g{f(x)}, YES the functions are inverse of each other.

Option B is the answer