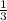Question

The cone in the diagram has the same height and base area as the prism. What is the ratio of the volume of the cone to the volume of the prism?

volume of cone/volume of prism = 1/2
volume of cone/volume of prism = 1/3
volume of cone/volume of prism = 2/3
volume of cone/volume of prism = 1
volume of cone/volume of prism = 3/2

Answer 1

we know that

the volume of the prism is equal to

`Vp=B*h`

where

B is the area of the base

h is the height of the prism

the volume of the cone is equal to

`Vc=(1)/(3) B*h`

where

B is the area of the base

h is the height of cone

Find the ratio of the volume of the cone to the volume of the prism

`ratio=(Vc)/(Vp) \\ \\ ratio=((1)/(3)Bh)/(Bh) \\ \\ ratio=(1)/(3)`

therefore

the answer is

`(1)/(3)`

Answer 2

The answer is volume of cone/volume of prism = 1/3. The volume of cone with height, h, and radius, r, is: V = 1/3πr^2h. If h = r, then V= 1/3πr^2 * r = V = 1/3πr^3. The volume of prism with height, h, and radius, r, is: V = πr^2h. If h = r, then V= πr^2 * r = V = πr^3. So, the volume of cone/volume of prism = 1/3πr^3 / πr^3 = 1/3.