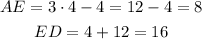Question

A-7. AB || CD, AB = 4, AE = 3x - 4,CD = 8, and ED = x + 12. FindAE and DE.-

Answer 1

AE = 8

DE = 16

Explanation:

We can determine that the triangles are similar by AAA congruence.

Therefore, we must calculate the ratio with the help of sides AB and CD, like this:

`\begin{gathered} r=(CD)/(AB) \\ \text{ replacing} \\ r=(8)/(4) \\ r=2 \end{gathered}`

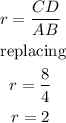
Now, we can establish the following equation to know the value of x:

`\begin{gathered} r=(ED)/(AE) \\ \text{ replacing} \\ 2=(x+12)/(3x-4) \\ \text{ solving for x:} \\ 2\cdot(3x-4)=x+12 \\ 6x-8=x+12 \\ 6x-x=12+8 \\ 5x=20 \\ x=(20)/(5) \\ x=4 \end{gathered}`

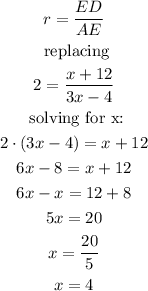
We replace the value of x to calculate the length of the sides AE and DE:

`\begin{gathered} AE=3\cdot4-4=12-4=8 \\ ED=4+12=16 \end{gathered}`