Question

The length of the longer leg of a right triangle is 6ft more than twice the length of the shorter leg. The length of the hypotenuse is 9 ft more than twice the length of the shorter leg. Find the side lengths of the triangle. Length of the shorter leg:Length of the longer leg:Length of the hypotenuse:

Answer 1

Given:

The length of the longer leg of a right triangle is 6ft more than twice the length of the shorter leg.

The length of the hypotenuse is 9 ft more than twice the length of the shorter leg.

Step-by-step explanation:

To calculate longer length:

Consider the shorter leg as s and longer leg as l.

As the longer leg of a right triangle is 6ft more than twice the length of the shorter leg, the longer leg can be represented as,

`l=6+2s\text{ . . . . . (1)}`

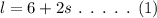
To calculate hypotenuse:

Now, consider the hyptenuse as h,

As the hypotenuse is 9 ft more than twice the length of the shorter leg, the hypotenuse can be represented as,

`h=9+2s\text{ . . . . . . (2)}`

To calculate shorter leg:

Using Pythagorean theorem, the shorter leg can be calculated as,

`\begin{gathered} h^2=l^2+s^2 \\ s^2=h^2-l^2\text{ . . . . . . (3)} \end{gathered}`

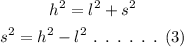
On plugging the equation (1) and (2) in equation (3),

`\begin{gathered} s^2=(9+2s)^2-(6+2s)^2 \\ s^2=9^2+(2s)^2+2(9)(2s)-\lbrack6^2+(2s)^2+2(6)(2s)\rbrack \\ s^2=81+4s^2+36s-36-4s^2-24s \\ s^2=12s+45 \\ s^2-12s-45=0 \end{gathered}`

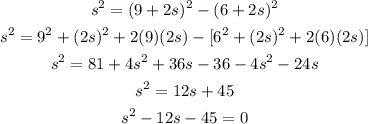
On solving the above quadratic equation,

`\begin{gathered} (s-15)(s+3)=0 \\ s=15,-3 \end{gathered}`

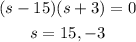
Since negative length is not a possible values, the value of shorter length of the right triangle is, s = 15 ft.

Substitute in equation (1):

On plugging the value of s in equation (1),

`\begin{gathered} l=6+2(15) \\ l=6+30 \\ l=36\text{ ft} \end{gathered}`

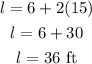
Substitute in equation (2):

On plugging the value of s in equation (2),

`\begin{gathered} h=9+2(15) \\ h=9+30 \\ h=39\text{ ft} \end{gathered}`

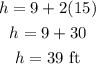
Hence,

Length of the shorter leg: 15 ft.

Length of the longer leg: 36 ft.

Length of the hypotenuse: 39 ft.