Question

The position of a particle on the x-axis at time t, t > 0, is s(t) = ln(t) with t measured in seconds and s(t) measured in feet. What is the average velocity of the particle for e ≤ t ≤ 2e? A. ln2 B. the quotient of 1 and the quantity of 3 times C. the quotient of the natural logarithm of 2 and e D. the quotient of the natural logarithm of 2 and 2

Answer 1

Option: C is the correct answer.

C. the quotient of the natural logarithm of 2 and e .

Explanation:

We are given a function s(t) that denotes the the position of a particle on the x-axis at time t, t > 0, as:

`s(t)=\ln (t)`

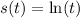
Now we are asked to find the average velocity of the particle for e ≤ t ≤ 2e.

We know that the average velocity is defined as the ratio of total distance to total time.

Now total distance covered in e ≤ t ≤ 2e is:

`s(2e)-s(e)`

`=\ln (2e)-\ln (e)`

`=ln (2e/e)`

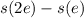
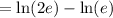
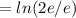
( Since,
`\ln (m)-\ln (n)=\ln (m/n)` )

`=\ln 2`

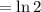
Also, total time is:

`2e-e=e`

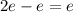
Hence, average velocity is:

`Average\ Velocity=(\ln (2))/(e)`

Option: C is the correct answer.

Answer 2

C. The quotient of the natural logarithm of 2 and e.

Explanation:

The position of a particle on the x-axis at time t, t > 0, is given by

`s(t) = \ln(t)`

with t is in seconds and s(t) is in feet.

The rate of change is,

=
`(f(b)-f(a))/(b-a)`

So rate of change of position or average velocity, for e ≤ t ≤ 2e will be,

`=(\ln2e-\ln e)/(2e-e)`

`=(\ln2e-\ln e)/(e)`

`=(\ln(2e)/(e))/(e)`

`=(\ln2)/(e)`

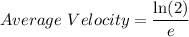
Therefore, option C is the correct answer.