Question

Please just give me the answer, I’m crushed of time

Answer 1

We have a parallelogram with vertices ar A(-10,5), B(-2,-3), C(2,3) and D(-6,1).

1) The midpoint of AB is:

`\begin{gathered} x_m=(x_a+x_b)/(2)=(-10+(-2))/(2)=-(12)/(2)=-6 \\ y_m=(y_a+y_b)/(2)=(5+(-3))/(2)=(2)/(2)=1 \end{gathered}`

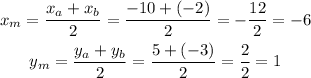
The midpoint of AB is (-6,1), not (-4,-6).

2) The midpoint of BC is:

`\begin{gathered} x_m=(x_c+x_b)/(2)=(2+(-2))/(2)=(0)/(2)=0 \\ y_m=(y_c+y_b)/(2)=(3+(-3))/(2)=(0)/(2)=0 \end{gathered}`

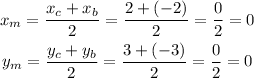
The midpoint of BC is (0,0).

3) The midpoint of CD is:

`\begin{gathered} x_m=(x_c+x_d)/(2)=(2+(-6))/(2)=(-4)/(2)=-2 \\ y_m=(y_c+y_d)/(2)=(3+1)/(2)=(4)/(2)=2 \end{gathered}`

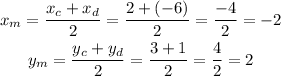
The midpoint of CD is (-2,2).

4) We have calculated the midpoint of CD in the previous point.

5) The diagonals bisect each other, so the intersection point is the midpoint of each diagonal.

Then, we find the endpoints of one of the diagonals, like A and C, and calculate the midpoint:

`\begin{gathered} x_m=(x_c+x_a)/(2)=(2+(-10))/(2)=(-8)/(2)=-4 \\ y_m=(y_c+y_a)/(2)=(3+(-5))/(2)=(-2)/(2)=-1 \end{gathered}`

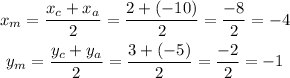
The intersection point is (-4,-1).

Answer: the statements that are true are:

(0,0) is the midpoint of BC.

(-2,2) is the midpoint of CD.

(-4,-1) is the intersection of the diagonals.