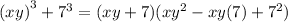Answer:
Given : Expression -
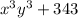
To find : How would the sum of cubes formula be used to factor given expression? Explain the process. Do not write the factorization.
Solution :
The formula of sum of cubes is,
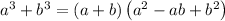
First we convert the given expression in
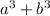
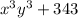
Apply exponent rule :
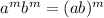
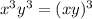
Rewrite
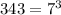
Therefore,
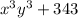 could be written as
could be written as
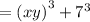
On comparison with the formula,
a=xy , b=7