Question

A student claims that when you double the radius of a sector while keeping the measure of the central angle constant, then you double the area of the sector. Do you agree or disagree?

Answer 1

In order to find if the student is correct or not, let's analyze the formula for the area of a circular sector:

`A=(r^2\theta)/(2)`

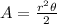
Where r is the radius and theta is the central angle.

If the radius is doubled, since it is squared, the area will be multiplied by 4 instead of being doubled as well:

`\begin{gathered} r^(\prime)=2r \\ A^(\prime)=(r^(\prime)^2\theta)/(2)=((2r)^2\theta)/(2)=(4r^2\theta)/(2)=4A \end{gathered}`

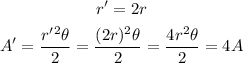
Therefore we disagree with the student.