Answer:
The exact circumference of a circle is,
 inches
inches
Explanation:
Area(A) and circumference(C) of the circle is given by:
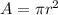
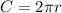
where, r is the radius of the circle.
As per the statement:
an area equal to 36 sq. in.
⇒A = 36 sq. in.
then;
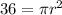
Divide both sides by
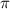 we have;
we have;
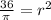
or
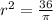
⇒
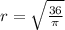
⇒
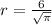
We have to find the exact circumference of a circle.
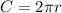
then;
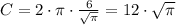
⇒
 inches
inches
Therefore, the exact circumference of a circle is,
 inches
inches