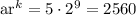Question

1 Use the sequence below to complete each task. 5, 10, 20, .. a. Identify the common ratio (r). b. Write an equation to represent the sequence. C. Find the 9th term (ay) Gina Wilon (All Things Algebra), 2013 Enter your answer's) here

Answer 1

a)

This is a geometrical sequence, which means that the common ratio is multiplied to get the next number in the sequence.

To calculate the common ratio of the sequence you have to divide one number of the set by the number below it:

`r=(10)/(5)=2`

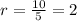
r=2

b)

"a" represents the first number of the set.

"ar" is the second number of the set

"arr" or "ar²" is the third value of the set

"ar³" is the fourth value of the set

You can repeat this as many times as you want, this is symbolized as "n-1" where n represents the number of times you repeat the multiplication and the "-1" is because the first value of the term is the only one you know and was determined before staring the sequence.

So you can calculate any value of the sequence as:

`ar^((n-1))`

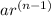
n is always equal or greater than 1.

To make it simpler you can replace n-1 with k, where k will represent the position in the sequence you wish to calculate:

`\text{ar}^k`

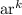
For k is equal or greater to zero.

c)

To find the 9th term of the sequence you have to use the formula above:

a=5

r=2

k=9

`\text{ar}^k=5\cdot2^9=2560`