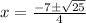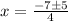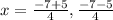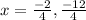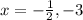Question

Decide which part of the quadratic formula tells you whether the quadratic equation can be solved by factoring:

A.) −b
B.) b^2 − 4ac
C.) 2a

Use the part of the quadratic formula that you chose above and find its value given the following quadratic equation:
2x^2 + 7x + 3 = 0

Answer 1

Part A - Option B -
`b^2-4ac`

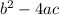
Part B -
`b^2-4ac=25`

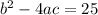
Explanation:

Part A : Decide which part of the quadratic formula tells you whether the quadratic equation can be solved by factoring.

The formula which tells the quadratic equation can be solve by factoring is called a discriminant.

Discriminant of the quadratic equation is
`D=b^2-4ac`

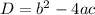
So, Option B is correct.

Part B : Use the part of the quadratic formula that you chose above and find its value given the following quadratic equation:

`2x^2 + 7x + 3 = 0`

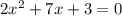
The solution of the quadratic equation
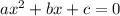`ax^2+bx+c=0` is

`x=(-b\pm √(D))/(2a)`

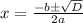
On comparing with
`2x^2 + 7x + 3 = 0`

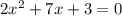
a=2 ,b=7 ,c=3

`D=b^2-4ac`

`D=7^(2)-4(2)(3)}`

`D=49-24`

`D=25>0`

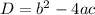
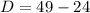
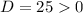
So, there exist distinct real roots.

Substitute in the formula,

`x=(-7\pm√(25))/(4)`

`x=(-7\pm 5)/(4)`

`x=(-7+5)/(4),(-7-5)/(4)`

`x=(-2)/(4),(-12)/(4)`

`x=-(1)/(2),-3`

Answer 2

The part of the quadratic formula that dictates whether the function is factorable or not is B. b^2 - 4ac. This determines the number of real, imaginary, negative and positive roots.
In the equation 2x^2 + 7x + 3,
we use the quadratic formula
x = -b +- sqrt (b2 -4ac) /2a = -7 +- sqrt (49 -24) /4
the answers are x1 =-0.5 and x2 = -3.